Prism Puzzler 3D Printing Project
I am so excited to share the process of our Prism Puzzler challenge. It was one of those learning tasks that just kept rolling. Each stage increasing in complexity and depth of thinking. Students were engaged, motivated, and demonstrating deep learning competencies throughout. The learning just made sense to students. They could visualize their learning and make connections during each stage. An educational WIN! When utilizing unconventional teaching strategies and methods, this does not always happen (refer to my first posts this year on failure) but it such a joy when thinks unfold as this did.
Specific Curriculum Expectations:
"Our shape only held 254 mL including the scale up. One of the problems might have been the bottom we made for the shape had to be covered up our hole, and we might have calculated wrong."
"Our design was too large for the printer therefore it was scaled down by 0.77. When we filled it with water it was 350ml but when we multiplied it by 0.77 it was equal to 430.5ml. This was fairly close to 500ml. A problem that we could have fixed was spending more time with the measurements of our design. The triangles were not exact to our measurements we calculated on the paper. So I think if we spent more time on the measurements, we would have been closer to 500ml."
"Was too big for the printer. The tinkercad design was too large for the style printer. It was scaled down by 0.75. When we created the design on tinkercad the edges were too thick and took up too much space.Also the formula was a very large decimal. Causing the shape to not hold the proper amount of water whether or not the calculations were correct or not.In the end It held 200 ml of water being scaled down 0.75.we could improve our design by possibly making the height higher."
Here are my key takeaways from the Prism Puzzler Challenge:
- Using a 3D printer to create tangible objects for students to think and reason with has more potential than I ever imagined. Something about holding and working with a novel object is highly motivating.
- Problem solving in mathematics that is driven by the design process enables students to approach challenging tasks with curiosity and the will to learn
- 3D printing allows students to test their solutions in the real world and make refinements based on those tests.
Specific Curriculum Expectations:
– solve problems that involve the surface area and volume of right prisms and that require conversion between metric measures of capacity and volume
– estimate and calculate the area of composite two-dimensional shapes by decomposing into shapes with known area relationships
– sketch different polygonal prisms that share the same volume
– determine, through investigation using a variety of tools and strategies the relationship between the height, the area of the base, and the volume of right prisms with simple polygonal bases and generalize to develop the formula
– determine, through investigation using a variety of tools, the surface area of right prisms
– estimate and calculate the area of composite two-dimensional shapes by decomposing into shapes with known area relationships
– sketch different polygonal prisms that share the same volume
– determine, through investigation using a variety of tools and strategies the relationship between the height, the area of the base, and the volume of right prisms with simple polygonal bases and generalize to develop the formula
– determine, through investigation using a variety of tools, the surface area of right prisms
– use estimation when solving problems involving operations with whole numbers, decimals, and percents, to help judge the reasonableness of a solution
– solve problems involving the multiplication and division of decimal numbers to thousandths by one-digit whole numbers,
I have to admit that many of these expectations were backwards mapped during and after the learning tasks. Our intentional learning goal was to solve problems involving the surface area and volume of prisms (right and non-right), but during the course of the activities so much more was addressed. Students were using computational skills during phase one to calculate of surface area and volume. They used conversions to determine volume dependent on capacity of water. During phase 2 they used ratios to determine height of prisms based on their calculation of area of the base. Some groups used estimation to judge if their solution was reasonable (this led to greater success for these groups and a next step for others). This is the uncomfortable part of tasks like this - you go in a bit blind - unsure of what learning MIGHT or MIGHT NOT occur. Afterwards many students commented that they liked that this learning was extremely challenging. I wonder if sometimes sticking solely with 'covering the curriculum' we miss the boat on providing challenge, and through challenge motivation and will to learn.
PHASE ONE
Team 4
Screen Capture Reflection

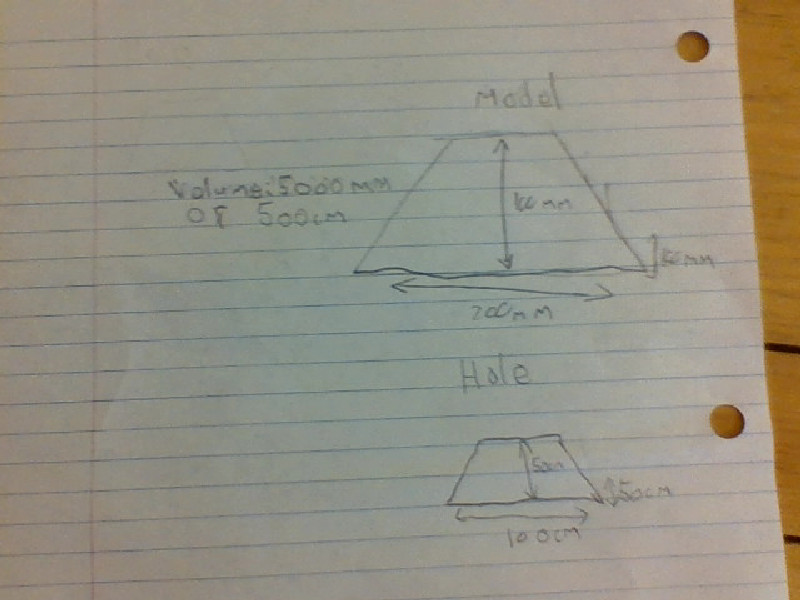 Observations:
Observations:
- "Will hold 500ml but shape will be twice as big for sturdy design."

Observations:
-500mL=500cm3 starting point
-Used reasoning to figure out 15x 10 as base
-Then figure out height from there
-Made volume larger by 100 to take into account width of container
Team 6
Screen Capture Reflection

Observations:
-all triangles to add up to 50cm2 so can easily multiply by 10 cm for height
-"So each triangle needs to be area of 6.25cm2"
PHASE THREE: TESTING & DEBUGGING
Team Reflections:
– solve problems involving the multiplication and division of decimal numbers to thousandths by one-digit whole numbers,
I have to admit that many of these expectations were backwards mapped during and after the learning tasks. Our intentional learning goal was to solve problems involving the surface area and volume of prisms (right and non-right), but during the course of the activities so much more was addressed. Students were using computational skills during phase one to calculate of surface area and volume. They used conversions to determine volume dependent on capacity of water. During phase 2 they used ratios to determine height of prisms based on their calculation of area of the base. Some groups used estimation to judge if their solution was reasonable (this led to greater success for these groups and a next step for others). This is the uncomfortable part of tasks like this - you go in a bit blind - unsure of what learning MIGHT or MIGHT NOT occur. Afterwards many students commented that they liked that this learning was extremely challenging. I wonder if sometimes sticking solely with 'covering the curriculum' we miss the boat on providing challenge, and through challenge motivation and will to learn.
PHASE ONE
Doug Braden from Inksmith came in to visit us and brought with him a collection of awesome 3D printed prisms. THANKS DOUG! Some were right prisms, others more irregular in shape. The first challenge for the students was to work in groups to determine the surface area and volume of one of these shapes.
This led to the discovery of a previously untapped potential of 3D printers on my part - not just for student design, but also for the creation of 'objects to think with'! The possibilities are endless!
PHASE TWO: TEAM CHALLENGE
Goal: To create a complex prism that will hold 500mL of water.
Task Outline:
-Create your detailed plan on paper first (sketch with labelled dimensions, explanations/justifications)
-Use TinkerCad to construct the rendering of your prism
-Create a screen capture using Nimbus [describe your rendering (dimensions, etc)]

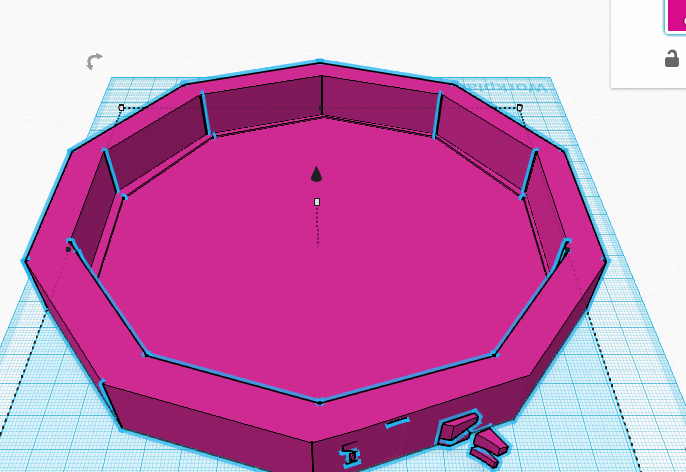
-Found formula for area on google (efficiency)
“We’re so close - are we close enough?” (precision/justification)
-found app which calculates any formula with each step

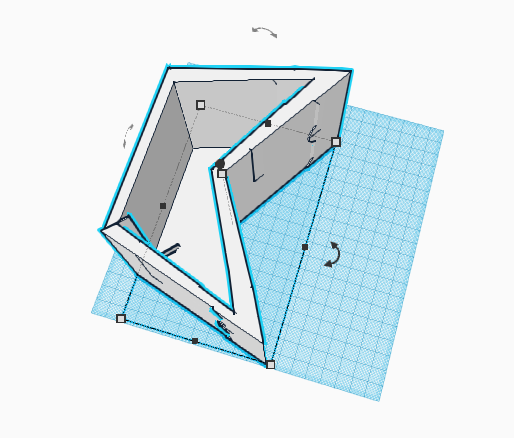
- next found 3 triangles that would add to 50cm2
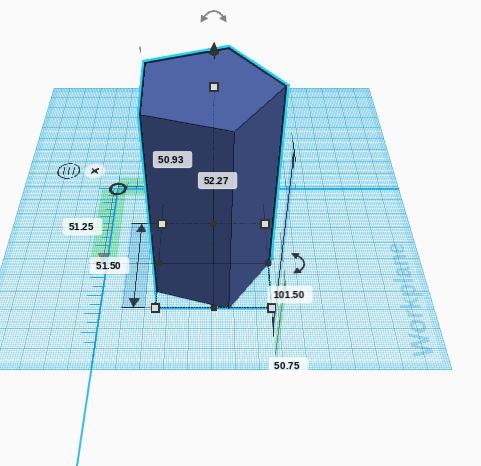 Observations:
Observations:
- "Let's do this!"
- 5.381cm2 as side lengths
- Found formula online to verify
This led to the discovery of a previously untapped potential of 3D printers on my part - not just for student design, but also for the creation of 'objects to think with'! The possibilities are endless!
 |
| Using specs and tangible object to determine surface area. |
 |
| Using understanding of capacity to uncover volume. |
 |
| Eureka! We discover that these two octagonal prisms (right and non-right) share the same volume. |
PHASE TWO: TEAM CHALLENGE
Goal: To create a complex prism that will hold 500mL of water.
Task Outline:
-Create your detailed plan on paper first (sketch with labelled dimensions, explanations/justifications)
-Use TinkerCad to construct the rendering of your prism
-Create a screen capture using Nimbus [describe your rendering (dimensions, etc)]
Team 1
Observations:
-using water bottle as a benchmark -Found formula for area on google (efficiency)
“We’re so close - are we close enough?” (precision/justification)
-found app which calculates any formula with each step
Team 2
Observations:
- base as 50cm height as 10cm- next found 3 triangles that would add to 50cm2
Team 3
- "Let's do this!"
- 5.381cm2 as side lengths
- Found formula online to verify
Team 4
Screen Capture Reflection
- "Will hold 500ml but shape will be twice as big for sturdy design."
Team 5
Observations:
-500mL=500cm3 starting point
-Used reasoning to figure out 15x 10 as base
-Then figure out height from there
-Made volume larger by 100 to take into account width of container
Screen Capture Reflection
-"So each triangle needs to be area of 6.25cm2"
PHASE THREE: TESTING & DEBUGGING
 |
| Let the testing begin! |
"Our shape only held 254 mL including the scale up. One of the problems might have been the bottom we made for the shape had to be covered up our hole, and we might have calculated wrong."
"Our design was too large for the printer therefore it was scaled down by 0.77. When we filled it with water it was 350ml but when we multiplied it by 0.77 it was equal to 430.5ml. This was fairly close to 500ml. A problem that we could have fixed was spending more time with the measurements of our design. The triangles were not exact to our measurements we calculated on the paper. So I think if we spent more time on the measurements, we would have been closer to 500ml."
"Was too big for the printer. The tinkercad design was too large for the style printer. It was scaled down by 0.75. When we created the design on tinkercad the edges were too thick and took up too much space.Also the formula was a very large decimal. Causing the shape to not hold the proper amount of water whether or not the calculations were correct or not.In the end It held 200 ml of water being scaled down 0.75.we could improve our design by possibly making the height higher."
Here are my key takeaways from the Prism Puzzler Challenge:
- Using a 3D printer to create tangible objects for students to think and reason with has more potential than I ever imagined. Something about holding and working with a novel object is highly motivating.
- Problem solving in mathematics that is driven by the design process enables students to approach challenging tasks with curiosity and the will to learn
- 3D printing allows students to test their solutions in the real world and make refinements based on those tests.
The Prism Puzzler 3D Printing Project is such an exciting and creative way to blend mathematics with hands-on learning. Projects like this make geometry feel practical and fun, especially when students get to see shapes transform into real models. For anyone struggling with the mathematical concepts behind 3D shapes, volume, and dimensions, exploring such projects can really boost understanding. And if the calculations or theory feel overwhelming, getting math assignment help can make the process easier and more enjoyable. This project is a great example of how innovative tools like 3D printing can make math both engaging and meaningful.
ReplyDelete